Analytical foundations
The derivation of analytical fundamentals for novel machine concepts is a major focus of our research work. In a current research project, for example, we are comprehensively dealing with the analytical fundamentals of the axial flux asynchronous machine. These include systems of equations for the determination of the air gap fields, the stray fields and the torques including all harmonics. A special challenge includes the analytical consideration of magnetically coupled sub-machines as they occur in an optimized stack. Based on these equation systems, we develop simulation models to investigate the operating behavior.
Analytical calculation methods for rotor loss determination in PSYM.
Concentrated stator windings (single tooth windings) in permanent magnet synchronous machines (PSYM) have cost and manufacturing advantages compared to distributed windings and also generate less ohmic losses due to the smaller winding heads. However, a concentrated rotating field winding generates a much wider variety of harmonic rotating waves with relevant amplitudes than a distributed rotating field winding, in addition to the main wave of current loading and induction. These harmonics sometimes lead to excessive eddy current losses in the permanent magnets, in the electrically conductive rotor bandages and in the rotor yokes, if these are of massive design. For the description and evaluation of these rotor losses, 2-dimensional analytical calculation methods have been developed at EWT for this type of machine.
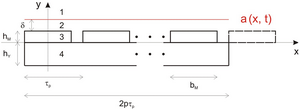
As an example, for a 10 kW machine with 10 poles and 12 slots and with one permanent magnet (Sm2Co17) per pole pitch, the current density distribution in tangential direction caused by the 7th harmonic of the stator current coating in one magnet is given opposite. The opposite 7th harmonic is the most damaging harmonic for this pole-number-groove-number configuration. The machine is loaded with the rated torque and runs at the rated speed of 2000 rpm. It operates with the 5th harmonic as the skin rotating shaft and has a laminated rotor yoke and no rotor banding. The eddy current power loss in all permanent magnets is 727 W.
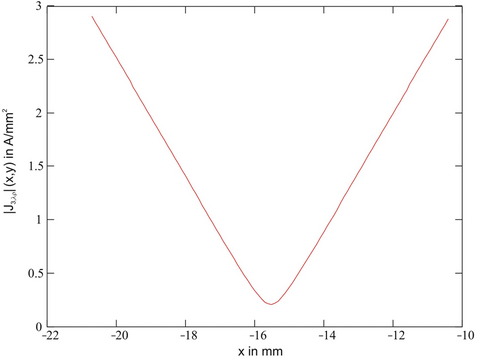
Segmentation of the permanent magnets in the tangential direction impedes the vortex flow in the individual magnet segments, which are electrically insulated from each other, and is thus an effective means of reducing the rotor power loss. As an example, the machine considered above is again considered under the operating condition defined there, but now each permanent magnet is divided in tangential direction into 4 equal segments each.
The current density distribution in a magnet segment in the tangential direction is shown opposite. The eddy current power loss in all magnet segments is now only 71 W.
Magnetic networks
Reluctance networks are an alternative to the finite element method (FEM). An electrical equivalent network simulates the magnetic circuit. With known flux paths and clever discretization, the calculation results obtained are equivalent to those of the FEM.
As part of a research project, this method is being extended to enable automated calculation of an electromechanical transducer. The time and calculation effort required is reduced to a few percent compared to a calculation using the FEM.
Winding Functions
The inductances in electromechanical energy converters can be determined by means of the winding functions. Here, both the winding scheme and the rotor position are taken into account. The aim of our research project is to create simulation models based on this calculation principle, which allow the effects of errors on the electrical quantities to be investigated. Conversely, this means that actually occurring faults in electromechanical converters can only be identified on the basis of the measurable terminal quantities.
